....:::: UNIVERSO SNIPER AIRSOFT ::::.... The Airsoft Trajectory Project: Efectos del Hop-Up

Sección III: Efectos del Hop-Up

La interacción de la fricción entre la goma del hop-up y la bola, incurre en un efecto de giro hacia atrás de la bola. Este efecto de giro, induce una fuerza ortogonal al movimiento de la bola, debido a una condición especial del Principio de Bernoulli, conocido como el Efecto Magnus. El efecto Magnus se debe a la interacción de alta velocidad entre la bola y el aire circundante. (Para simplificar, el giro de aquí en adelante se refiere particularmente al efecto de giro)

A menudo se debate sobre qué fuerza es más responsable del efecto de la elevación, el Principio de Bernoulli o el Efecto Magnus. Técnicamente, el Principio de Bernoulli trata la presión baja debido a que un objeto se mueve sobre un medio a alta velocidad (o el medio que se mueve sobre el objeto). La Elevación de Magnus se atribuye con mayor precisión al cambio de momento de la capa límite, debido a las áreas variables de baja presión alrededor del objeto, cuyo efecto causa un movimiento neto del objeto en la dirección opuesta al movimiento de la capa límite. Ambas causan una elevación en las bolas, sin embargo, los efectos de cada una dependen significativamente de: 1) la velocidad del objeto a través de un medio, y 2) la velocidad de rotación del objeto.

Cuando un objeto esférico relativamente liso gira a una velocidad baja en relación con su movimiento hacia adelante, el aire circundante es bastante laminar. El flujo laminar estable induce la separación temprana de la capa límite, que conduce a un gran campo de estela que induce un área de baja presión inmediatamente detrás de la bola (incurriendo en lo que se conoce como resistencia a la presión). Esto no solo afecta el arrastre general experimentado por la esfera, sino que el flujo laminar suave también tiene un efecto adverso en la elevación. Mientras que el efecto de conregiro causa un área de baja presión sobre la esfera debido al Principio de Bernoulli, una velocidad de rotación relativamente baja conduce a un cambio hacia arriba en la capa límite, negando el levantamiento debido al Principio de Bernoulli y, en última instancia, causando un levantamiento negativo. Esto se conoce como el efecto Magnus inverso. En consecuencia, las bajas velocidades de giro proporcionan dos inconvenientes a la trayectoria de mayor resistencia al avance y al retroceso.

Cuando la velocidad de giro es alta en relación con el movimiento hacia adelante, el aire circundante se vuelve turbulento. El flujo de aire turbulento, que normalmente aumenta la resistencia de los objetos aerodinámicos, en realidad sirve para aumentar el flujo de aire sobre la esfera relativamente no aerodinámica, lo que hace que la capa límite siga el contorno de la superficie de la esfera por más tiempo. (Esta es la misma razón por la que las pelotas de golf tienen hoyuelos, para inducir un flujo turbulento que finalmente disminuye el número de Reynolds). El flujo de aire turbulento reduce al mínimo el campo de activación y, en última instancia, disminuye el arrastre de presión. Además, el giro hace que la capa límite experimente un movimiento hacia abajo en relación con la posición de los proyectiles. Esto conduce a una fuerza neta de elevación sobre la esfera como el cambio de momento de la capa límite conocida como la Elevación de Magnus. Cuanto mayor sea la velocidad de giro en relación con el movimiento hacia adelante, mayor será el área de menor presión sobre la esfera y mayor será el cambio de momento y, por lo tanto, mayor será el efecto de la Elevación de Magnus.

Al salir del cañón, la bola tiene una velocidad concreta y una velocidad de giro específica, que se traducen en velocidad lineal (U) y velocidad de rotación (V), respectivamente. Además, ambas velocidades comienzan a mostrar una caída exponencial, a medida que la velocidad lineal disminuye debido al arrastre, mientras que la velocidad de rotación disminuye debido a la fricción de la superficie. A medida que la velocidad lineal disminuye a una tasa mayor que la de la velocidad de rotación, la relación de velocidad de rotación con la velocidad lineal, V/U, aumenta.

Un intercambio de fricción perfecto entre la bola y la goma del hop-up, daría como resultado una V/U inicial de 1. Aunque el intercambio de fricción es muy eficiente, simplemente no es posible tener un intercambio de fricción perfecto. Además, la bola no ha alcanzado su velocidad máxima, ya que hace contacto con la goma del hop-up tal como va realizando su tránsito a través del cañón (aunque la velocidad de rotación aumentará ligeramente a medida que gira por el cañón). Para la mayoría de los cálculos, V/U se limitó a 0,41. Para una bola de 0.20 g disparada a 328 fps (o el equivalente de 1 julio), una V/U de 0.41 se traduciría en una velocidad de giro de 132.000 revoluciones por minuto. En comparación, una bala típica deja el cañón girando entre 200,000 rpm y 300,000 rpm. Para las balas, el giro es directamente proporcional a la velocidad lineal y se calcula fácilmente multiplicando la velocidad de salida por la relación de giro. Por ejemplo, una bala del 7.62, podría tener una velocidad de salida de 2800 fps, con una relación de giro de 1:8. En este caso, podría tener un giro de más de 250,000 rpm. (Casualmente, muchas balas comienzan a sufrir problemas de inestabilidad debido a una falla estructural del encamisado por encima de las 400,000 rpm). Mientras que las balas se mueven a velocidades mucho más altas que las bolas, estas son significativamente menos densas y tienen un momento de inercia más bajo que el de las balas, por lo que las bolas son capaces de recibir giros tan altos a velocidades relativamente bajas.

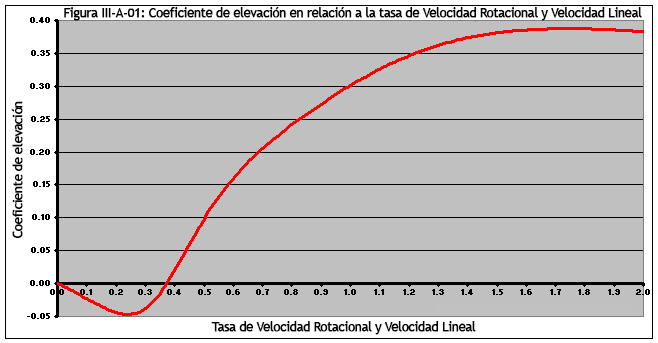
La Figura III-A-01 ilustra la cantidad de elevación generada proporcional a la relación V/U. Por debajo de una V/U de 0.37, el coeficiente de elevación es en realidad negativo: cualquier cosa por debajo de una relación de 0.37 está sujeta al efecto Magnus inverso. Por encima de 0.37, la elevación es positiva. Incluso si la bola dejara el cañón a una V/U inferior a 0,37, la velocidad lineal generalmente disminuye a una velocidad mayor que la velocidad de rotación, lo que hace que V/U aumente a medida que la bola sigue su trayectoria. Si la velocidad de rotación fuera constante, la bola iría más alta en el aire. Una configuración ideal de hop-up intentará lograr un coeficiente de elevación que crezca en relación con la gravedad (aunque no sea tan alto como para causar un arco alto), proporcionando así una trayectoria aparentemente plana.

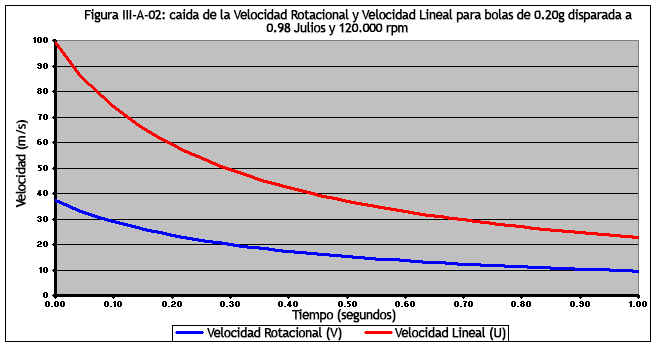
Para explicar cómo V/U afecta el movimiento vertical neto de la bola, he generado cuatro gráficos que muestran cómo la velocidad de rotación (V), la velocidad lineal (U), el coeficiente de elevación (CL) y la fuerza neta experimentada por una bola de 0.20g disparada a 325 fps con giro de 120.000 rpm.

En la figura III-A-02, podemos ver cómo la velocidad lineal disminuye rápidamente (en comparación con la velocidad de rotación).

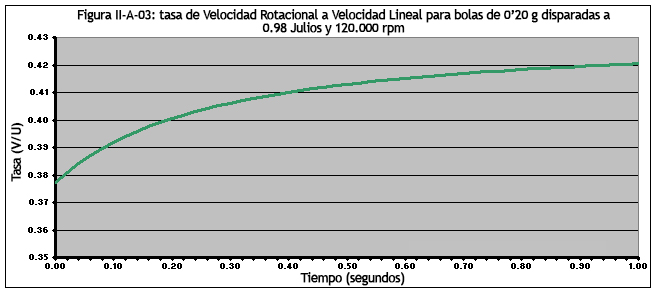
Como U disminuye más rápido que V, vemos que la relación V/U aumenta como se muestra en la Figura III-A-03.

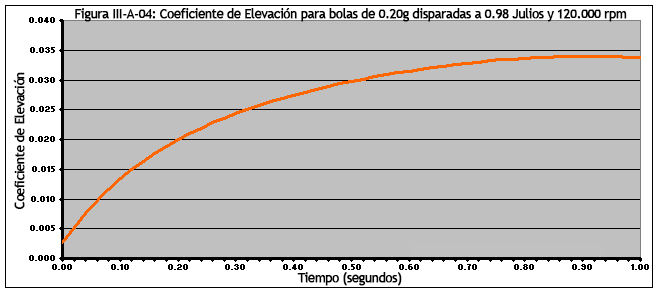
En la Figura III-A-04, podemos ver cómo V/U contribuye a la elevación, y se genera una elevación positiva durante bastante tiempo. Mientras que el coeficiente de elevación aumenta constantemente, la velocidad de avance (U) disminuye rápidamente, lo que se traduce en una menor fuerza de elevación a distancia.

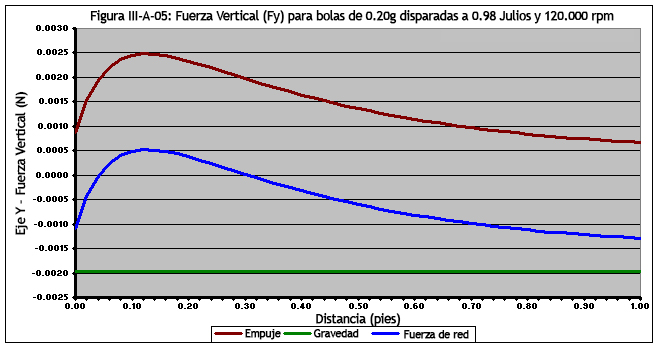
En la Figura III-A-05, podemos ver cómo las fuerzas opuestas de la elevación (FL) y la gravedad (Fg) afectan la fuerza vertical general (Fy) sobre la bola. Durante los primeros 0.04 segundos, la bola se está moviendo hacia abajo. Durante los siguientes 0.26 segundos, la bola está acelerando hacia arriba. Después de 0,30 segundos (y una distancia total de aproximadamente 67 pies, 20.4 metros), la bola comienza una aceleración hacia abajo. Ten en cuenta que aunque la bola está acelerando hacia abajo, eso no significa que su velocidad sea hacia abajo, sino que tiene una velocidad positiva que está disminuyendo rápidamente. La bola no comienza a moverse hacia abajo hasta después de que hayan transcurrido aproximadamente 0.51 segundos (o aproximadamente 96 pies de distancia, ó 29.2 metros).

La Figura III-A-06 muestra los efectos del hop-up sobre la bola. Observa que a 0 revoluciones por minuto (rpm), la bola experimenta una trayectoria parabólica normal. A 36,000 rpm, V/U es lo suficientemente bajo como para que la elevación sea negativa debido al Efecto Magnus inverso; Dado que la fuerza es negativa (es decir, hacia abajo), ayuda a la gravedad a hacer que la bola. A 72.000 rpm, el efecto Magnus inverso es aún más alto, lo que provoca una trayectoria marcadamente descendente. < A alrededor de 100.000 rpm, el Efecto Magnus comienza a tener efecto causando una elevación positiva, proporcionando una trayectoria más cercana a la de una bola disparado sin giro. A 115,000 rpm, la trayectoria parece plana debido a que los efectos de la gravedad se niegan marginalmente debido a la Fuerza Magnus, mientras que las rpm más altas causarán que la bola haga un arco hacia el cielo.

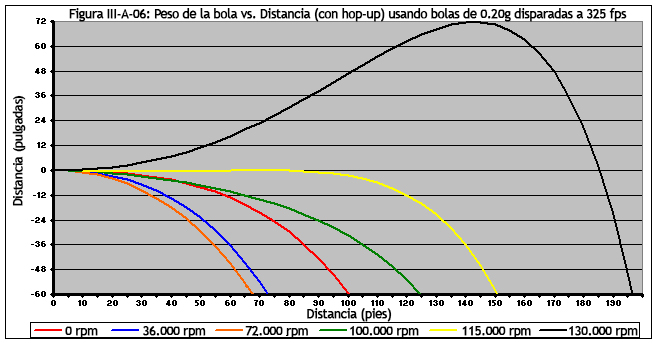
Si bien la trayectoria de la bola parece ser casi perfecta a 90 pies (30 metros) si se dispara a ~ 115,000 rpm, en realidad la interacción del hop-p no siempre genera un giro que es perfectamente perpendicular al suelo a lo largo del eje z (dirección horizontal) perpendicular al fusil). Dos razones para esto podrían ser el tirador que sostiene el rifle con inclinación o la bola está ligeramente descentrada contra la goma dle hop-up.

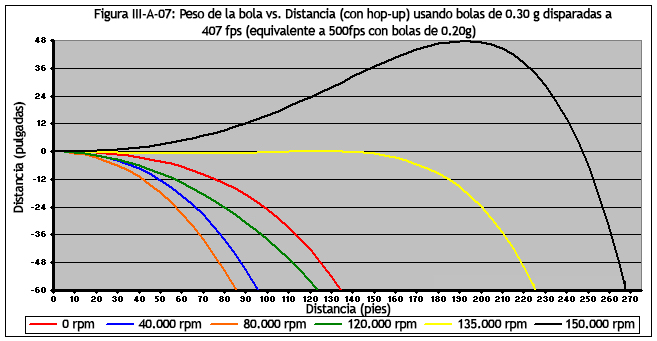
La Figura III-A-07 muestra los efectos del hop-up en una bola de 0.30 g disparada a 407 fps. Nuevamente, vemos que el efecto Magnus inverso causa un rendimiento degradado si el hop-up no está activado pero no es lo suficientemente alto como para generar una alta V/U. También se debe tener en cuenta que las gráficas se exageran a lo largo del eje y, mientras que la trayectoria degradada de los disparos realizados con un hop-up bajo es evidente en la gráfica, no sería tan visible en la observación real. < A 135,000 rpm, vemos una trayectoria relativamente plana, mientras que a 150,000 rpm vemos una trayectoria que muestra un arco mayor por encima del punto objetivo. Mientras que el disparo de 150,000 rpm proporcionará un mayor alcance, el valor de 135,000 rpm sería más deseable ya que proporcionaría una trayectoria más plana. Nuevamente, el eje es exagerado: el arco no parece tan obvio en la realidad.

La Figura III-A-08 muestra cómo una cantidad igual de giros afecta a varias bolas pesadas cuando se disparan a energías iguales. La razón por la que las bolas pesadas generan más sustentación es que, para energías de salida en boca iguales, las bolas más pesados tienen una velocidad lineal más baja. Esto significa que la relación V/U es mayor.

Esta información puede parecer contradictoria al principio. Parece como si un jugador necesitara disminuir la cantidad de hop-up cuando se usan bolas más pesadas, a diferencia de la realidad en la que el hop-up generalmente se incrementa cuando se usan bolas más pesadas. El problema radica en pensar que una configuración de hop-up no modificada produciría velocidades de giro iguales, sin embargo, esta es una suposición incorrecta. < Debido a que las bolas más pesadas tendrán un momento de inercia más alto, se necesita más esfuerzo de torsión para generar una cantidad igual de giro. Por lo tanto, aunque una configuración particular puede estar bien para una bola de 0.25 g, el uso de una bola de 0.30 g sin modificar el hop-up no generará un par suficiente para inducir un giro adecuado en la bolita de 0.30 g. < Por ejemplo, una configuración de hop-up que da como resultado 100,000 rpm de giro en una bola de 0.25 g, puede generar solo 80.000 rpm con una bola de 0.30 g, ya que una bola más pesada ajustada al hop-up no producirá el esfuerzo de torsión adecuado para lograr la cantidad deseada de giro.

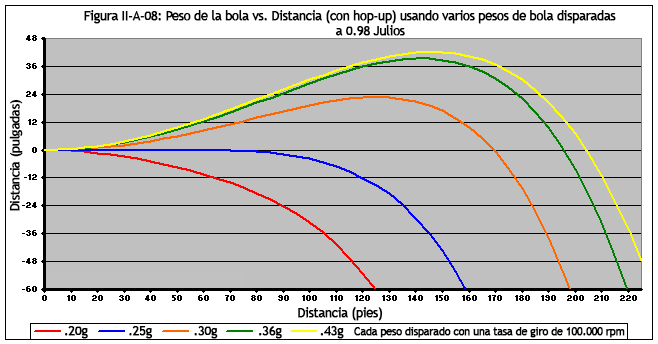
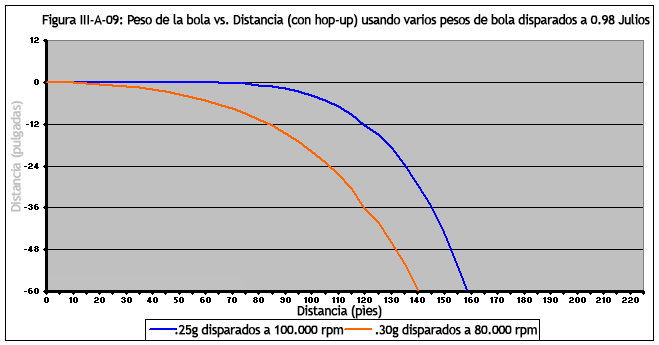
La Figura III-A-09 proporciona una estimación de cómo una unidad de hop-up correctamente configurada para bolas de 0.25 g puede producir un sub par para bolas más pesadas.

La Figura III-A-10 muestra cómo la velocidad afecta la trayectoria cuando se aplica el hop-up. A velocidades lineales más bajas, V/U es alta y da como resultado un arco drástico hacia el cielo en la trayectoria de la bola. A velocidades lineales más altas, la fuerza de elevación es insuficiente, ya que V/U es demasiado baja. Se debe tener en cuenta que, para configuraciones de hop-up iguales, una velocidad en boca más alta resultará en mayores tasas de giro. (es decir, una configuración de hop-up que genera 95,000 rpm cuando una bola de 0.20 g pasa a 300 fps podría generar 125,000 rpm si la misma bola pasa a 400 fps), lo que significa que el upgrade de tu arma lúdico deportiva alterará la trayectoria, sin embargo no hay que ser tan drástico como se muestra a continuación, debido a mi uso de velocidades de giro constantes. < Debo tener en cuenta que un disparo de 200 fps con un giro inicial de 95,000 rpm tendría una V/U muy alta, y la trayectoria que se muestra a continuación para el disparo de 200 fps es probablemente imposible, ya que sería muy difícil generar un giro tan alto desde Un disparo de relativamente poca energía.

Modelar la trayectoria en relación con el hop-up resultó ser una tarea mucho más desafiante que cualquier otro factor que contribuya a la trayectoria. El cálculo de los coeficientes de sustentación, así como la relación entre las velocidades de rotación y las velocidades lineales, y posteriormente la Fuerza Magnus, fueron componentes clave que son razonablemente fáciles de calcular. No tuve suerte en encontrar los coeficientes necesarios para calcular la velocidad a la que cae el giro debido a la fricción de la superficie. Además, la recopilación de datos empíricos no ayudó, ya que era muy difícil lograr resultados perfectamente consistentes del mecanismo del hop-up de un rifle (muy probablemente debido a la variación en la energía del cañón de un disparo a otro), y las observaciones visuales fueron altamente subjetivas; a un observador le resultaría difícil discernir entre una trayectoria relativamente plana y una que se elevó más de 25 cm por encima de la horizontal en su vértice. El hop-up como se muestra a lo largo de estas páginas, no debe tomarse como un evangelio, están muy cerca pero no son perfectos. Una cosa que no se tuvo en cuenta en el modelado del hop-up, es la disminución de la velocidad de salida debido a la pérdida de energía de la bola al rozar el caucho del hop-up.

Todo el texto, imágenes, y enlaces son propiedad de cybersloth.org y no serán reproducidos sin permiso. Para más información: airsoft@cybersloth.org.

Traducción al castellano por Daniel "Sniper" Muñoz, Universo Sniper Airsoft

The Airsoft Trajectory Project