Sección V-A-02: Componente viento cruzado
El componente de viento cruzado se toma como el componente del viento perpendicular a la línea trazada desde el rifle hasta el objetivo. Al igual que se hizo con el componente viento en contra / viento de cola, el viento cruzado debe reducirse del componente viento total a un vector. Esto se hace tomando la dirección del viento en relación con la dirección original del objetivo.
|
La figura V-A-02-a ilustra cómo dividir la dirección del viento en componentes. En este caso, el viento sopla a diez millas por hora en un ángulo de 120° con respecto a la dirección apuntada. Esto significa que la bola experimentará un viento en contra de cinco millas por hora y un viento cruzado de 8.6 millas por hora. Para calcular la desviación debido al viento cruzado, solo debemos preocuparnos por el componente de viento cruzado, ó 8.6 mph.
El siguiente problema es determinar cuánto afecta el viento a la trayectoria. Esto se puede calcular fácilmente utilizando la ecuación de arrastre en la Sección I-D-01. La cantidad de desviación estará determinada por la velocidad lateral de la bola. A su vez, la velocidad lateral depende de cuánto tiempo ha estado sometido la bola al viento cruzado y con qué rapidez se está moviendo el viento en relación con la bola (o durante cuánto tiempo y qué aceleración experimenta la bola...)
La mayoría de las personas tienden a adherirse a cualquiera de las dos teorías acerca de por qué una bola se verá o no afectada por el viento cruzado. La primera teoría es que las bolas más pesados conservarán mejor su inercia, por lo que se verán menos afectados por el viento cruzado. A partir de ese momento, las bolas más pesadas experimentarán un menor grado de desviación lateral.
La segunda teoría es que todas las bolas, independientemente del peso, serán "atrapadas" por el viento y se moverán aproximadamente a la misma velocidad lateral que la del medio por el que están pasando. |
Figura V-A-02-a:
Diagrama de Componente de Viento |
La mayoría de los tiradores al blanco adoptan este último argumento. Esto es comprensible, ya que hace que el cálculo de la desviación del viento sea muy fácil. Además, la mayoría de los tiradores están tratando con un proyectil muy denso, disparado a una velocidad muy alta.
Desafortunadamente, esta última teoría es incorrecta. Los usuarios de armas de aire comprimido de perdigones del 4.5 y bolas de acero, pueden salirse con la suya hasta cierto punto porque, nuevamente, se trata de un proyectil denso que se mueve a una velocidad muy alta. Tanto para los plomos como para las bolas de acero, el proyectil alcanza el objetivo con relativa rapidez. Además, la mayor densidad (y masa) de ambos tipos de proyectiles, dictan que la fuerza necesaria para acelerar lateralmente el proyectil debe ser significativamente mayor.
Sin embargo, este NO ES el caso de los jugadores de airsoft, ya que el proyectil tiene una densidad mucho menor que la de un perdigón (o incluso una bola de acero del 4.5) y las velocidades del cañón tienden a ser considerablemente menores para los rifles del airsoft, en comparación con las velocidades de armas de fuego y armas de aire comprimido de perdigonas del 4.5. Para ilustrar este punto, consideremos el siguiente ejemplo:
Imagina que un jugador está disparando a un objetivo que está a 100 pies/30.4 metros de distancia, y que está disparando bolas de 0.20g a 275 fps, con un viento cruzado de 20 mph/32.1 kmh. Si el tirador estima que la velocidad promedio de la bola será de 160 pies por segundo/48.7 metros por segundo (lo que en realidad es correcto), entonces pueden esperar fácilmente que a la bola le tome alrededor de 0,70 segundos para alcanzar el objetivo (nuevamente, los cálculos reflejan la realidad). Si el la bola mantiene una velocidad lateral constante de 20 mph/32.1 kmh (o aproximadamente 30 pies por segundo/9.1 metros por segundo) desde el momento en que abandona el cañón, se desviará 21 pies/6.4 metros hacia el lado para cuando haya recorrido 100 pies/30.4 metros. 21 pies/6.4 metros es una gran cantidad; creo que la mayoría de los jugadores de airsoft que realizan pruebas en un viento de este tipo, determinarían rápidamente que la desviación lateral es significativamente menor que 21 pies/6.4 metros. En realidad, la bola solo se desviaría aproximadamente 22 pulgadas/55.8 cm, muy lejos de los 21 pies/6.4 metros estimados anteriormente. ¿Por qué la gran discrepancia? Como se ilustrará a continuación, la bola no se mueve a 20 mph/32.1 kmh al salir del cañón, de hecho, ni siquiera se acerca a las 20 mph/32.1 kmh.
Las Figuras de la V-A-02-b a la V-A-02-e, muestran las características laterales de diferentes bolas que han sido disparadas a 0.70 Julios (o el equivalente de 275 fps con bolas de 0.20g) en un viento cruzado de 20 mph/32.1 kmh.
La aceleración de arrastre es una función de la masa, y como tal, esperaríamos que las bolas con una masa más alta, experimentaran una aceleración menor. La figura V-A-02-b muestra la aceleración lateral de una variedad de pesos de bolas. En consecuencia vemos que las bolas de 0.20 gramos experimentan una aceleración más pronunciada debido al viento cruzado. Observa también que la aceleración disminuye con el tiempo y la distancia. La razón por la que la aceleración disminuye con el tiempo es que la bola experimenta menos resistencia con el paso del tiempo. Piénsalo de esta manera: cuando la bola abandona el cañón, está sujeta a un arrastre, que es un componente de la velocidad del viento en relación con la bola. Inmediatamente después de abandonar el cañón, la bola está experimentando resistencia debido a una velocidad de viento lateral de 20 mph (ó 8.94 m/s ó 29.33 fps). A medida que pasa el tiempo, la bola comienza a formar parte del medio en movimiento. A medida que esto sucede, la velocidad del viento lateral en relación con la bola disminuye, reduciendo así la fuerza de arrastre lateral.

En la Figura V-A-02-c, vemos la velocidad lateral de la bola en millas por hora. Inicialmente, todas las bolas tienen una velocidad lateral de 0 mph. A medida que pasa el tiempo, la velocidad lateral de la bola aumenta a medida que aceleran lateralmente. Ten en cuenta que a 100 pies/30.4 metros, las bolas de 0.20 gramos se moverán lateralmente a aproximadamente 4.1 mph/6.5 kmh. Por el contrario, observa que la bola de 0.43 gramos se mueve lateralmente a aproximadamente 2.2 mph/3.5 kmh. Es fácil ver por qué las bolas más pesadas se desempeñan mejor con vientos más fuertes que las bolas más livianas.
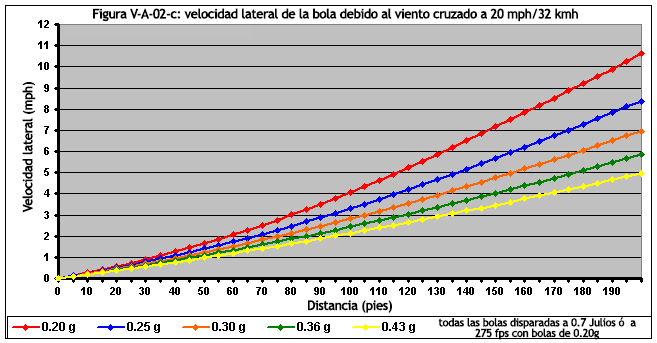
Para el gráfico de velocidad, decidí mostrar las velocidades laterales a una distancia de 200 pies. La razón por la que hice esto fue para ilustrar que incluso las bolas de 0.20 gramos relativamente ligeras, no alcanzarán una velocidad de 20 mph a una distancia de 200 pies. En realidad, el proyectil nunca alcanzará las 20 millas por hora, ya que la aceleración lateral disminuye constantemente debido a una fuerza de arrastre que disminuye continuamente. Esto podría parecer contradecir el hecho de que la aceleración lateral está disminuyendo con el tiempo, sin embargo, solo aparece de esta manera porque la gráfica anterior se generó como velocidad frente a distancia. En una gráfica de la velocidad en función del tiempo, podemos ver claramente que la velocidad lateral está disminuyendo, como se muestra en la Figura V-A-02-d.
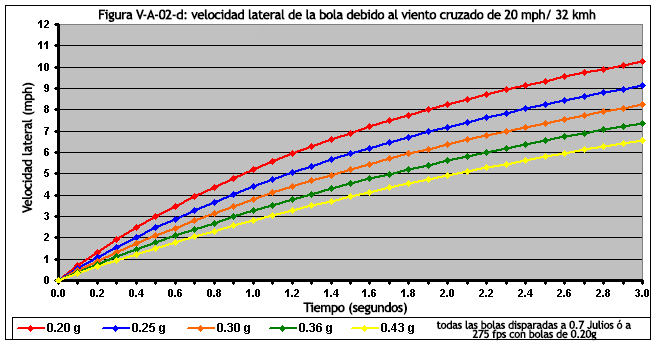
Para el análisis de velocidad frente al tiempo, decidí mostrar las velocidades laterales para un modelo largo de 3 segundos. Sin embargo, esto es completamente académico, ya que es imposible que una bola de orientación horizontal, permanezca en el aire durante tres segundos. Sin embargo, sí ilustra el hecho de que el proyectil no alcanzará las 20 mph después de un tiempo de vuelo muy largo. Solo por el bien de la discusión, realicé un modelo extremadamente largo que se acotó a 25 segundos. Aquí están los resultados:
| Tiempo(segundos) | Velocidad (m/s) | Velocidad (mph) | |
| 0 | 0.00 | 00.0 | |
| 5 | 5.54 | 12.4 | |
| 10 | 6.84 | 15.3 | |
| 15 | 7.42 | 16.6 | |
| 20 | 7.75 | 17.3 | |
| 25 | 7.96 | 17.8 |
Nuevamente, a medida que aumenta la velocidad lateral del proyectil, la velocidad del viento en relación con el proyectil disminuye, reduciendo la cantidad de arrastre que experimenta el proyectil. Otra ejecución del modelo que realizó cálculos a 50 segundos mostró que la bola, todavía estaba por debajo de 19 mph a 50 segundos.
Finalmente, en la Figura V-A-02-e, podemos ver la desviación real de las bolas. Incluso las de 0.25 gramos muestran una marcada reducción en la deflexión lateral en comparación con la de los 0.20 gramos. Sin embargo, aumentar la masa de la bola, se convirtió en una ley de rendimientos decrecientes. La diferencia en la desviación lateral entre la de 0.30 gramos y la de 0.43 gramos es de solo aproximadamente cuatro pulgadas a una distancia de 100 pies. Y esto es cuando se dispara a 275 fps. Como veremos, a velocidades más altas, las diferencias entre los pesos se reducen a distancias más cortas.
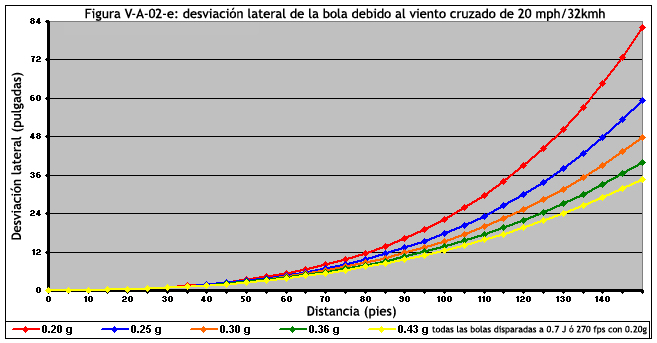
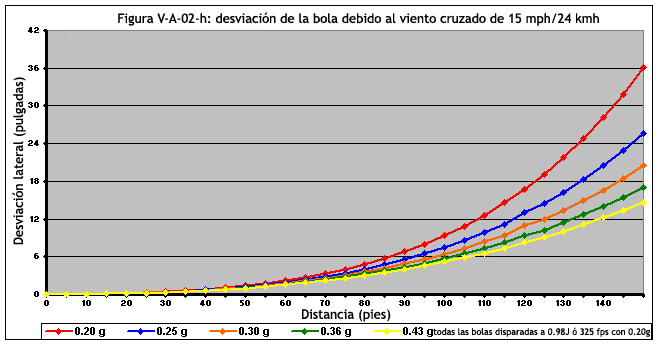
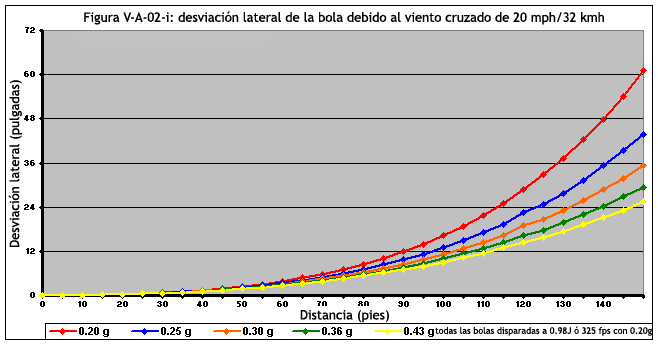
Las figuras de la V-A-02-f a la V-A-02-i tratan de proyectiles disparados a 0,98 Julios (ó 325 fps con bolas de 0.20g)
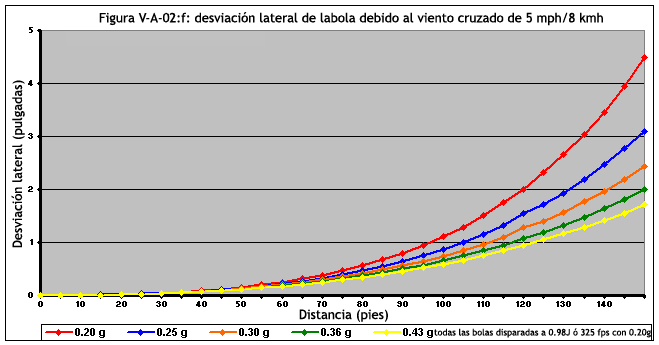

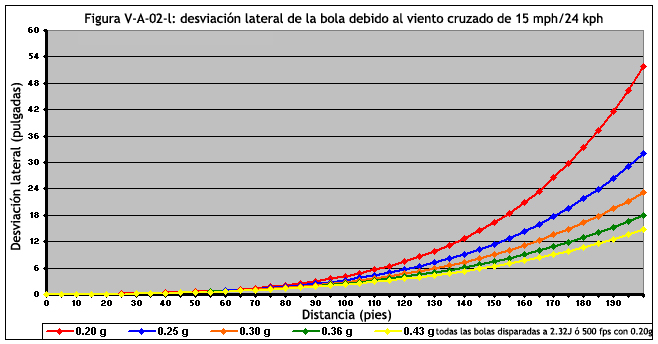
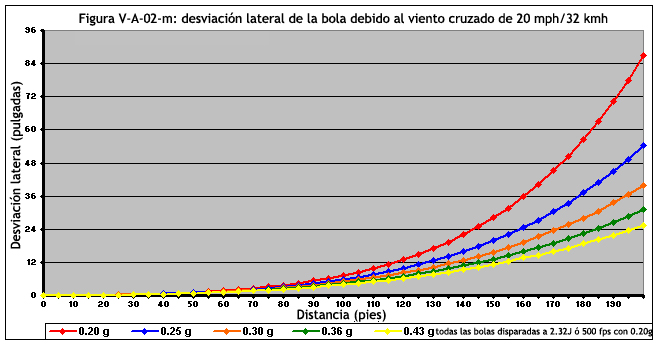
Las figuras de la V-A-02-j a la V-A-02-m estudian a proyectiles disparados a 2.32 Julios (ó 500 fps con bolas de 0.20g)


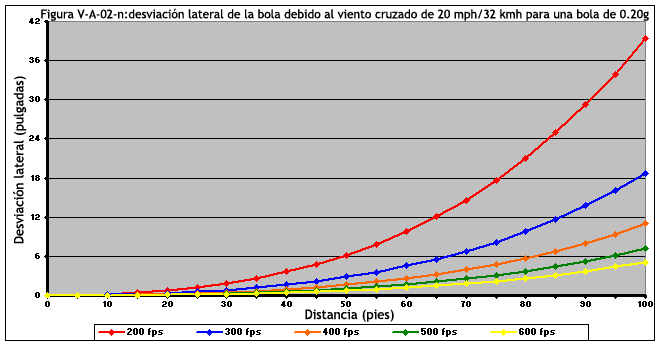
Por último, la Figura V-A-02-n muestra cómo hay una relación entre la velocidad de salida y el viento cruzado. Podemos ver que para pesos de bola iguales, un disparo de alta potencia alcanzará su objetivo al haber experimentado menos desviación. Por ejemplo, si estuviera disparando a un objetivo a 100 pies de distancia con un viento cruzado de 20 mph, una bola de 0.20 g disparada a 400 fps, solo se habrá desviado aproximadamente 11 pulgadas, mientras que un disparo de 300 fps se habría desviado aproximadamente 19 pulgadas.
Ten en cuenta que durante un período de tiempo igual, la bola se mueve lateralmente la misma distancia para cada disparo. Los disparos de alta potencia no resisten el viento cruzado mejor que los disparos de baja potencia; más bien, los disparos de alta potencia se alejan más en menos tiempo. Para explicarlo más a fondo, el disparo a 600 fps alcanza los 100 pies después de 0,32 segundos, tiempo después del cual se desvió aproximadamente 5 pulgadas. Después de 0.32 segundos, el disparo de 500 fps solo ha avanzado 90 pies, donde tiene una desviación igual de 5 pulgadas. Por el contrario, el disparo de 200 fps solo alcanza los 47 pies en el transcurso de 0,32 segundos.
|
Todo el texto, imágenes, y enlaces son propiedad de cybersloth.org y no serán reproducidos sin permiso. Para más información: airsoft@cybersloth.org. Traducción al castellano por Daniel "Sniper" Muñoz, Universo Sniper Airsoft The Airsoft Trajectory Project Copyright © 2005-2006 cybersloth.org - 2013, Universo Sniper Airsoft Todos los derechos reservados |

