Sección VIII: Comentarios de cierre

El estudio de las trayectorias de las bolas ha sido tanto desafiante como interesante.  Ha habido muchas cuestiones que no sabía responder cuando me decidí a crear esto, y todavía hay otras preguntas que creía saber la respuesta, sólo para darme cuenta de que estaba completamente equivocado.  It has taken a lot of testing, a lot of help, and a lot of communication to come up with the right model parameters. En general, estoy bastante contento con los resultados, así como con el proceso de aprendizaje, y espero que otros también lo encuentren útil. 

Si has leído los datos y no has podido encontrar la respuesta a las preguntas iniciales publicadas en la página de introducción, aquí están nuevamente, completas con respuestas cortas (o tan cortas como sea posible) y enlaces a más en explicaciones en profundidad. 

¿Las bolas de 8 mm resisten el viento mejor que las de 6 mm?

¿Las bolas a alta velocidad resisten el viento mejor que los que van a baja velocidad?

No hay una respuesta simple a esta pregunta ... en última instancia, depende de tus preferencias individuales. Esperemos que todos los datos te ayuden a determinar si vale la pena upgradearla o no. 

Para energías de salida en boca iguales, que bola llega más lejos, ¿la de 0,20g ó la de 0,25 g?

Uno de los debates clásicos, aparentemente interminables que surge, es si la bola de 0.20g supera a la de 0.25g. Dadas las energías en boca iguales para las bolas, disparados sin hop-up, la bola más pesada siempre superará a la más ligera. Hay dos razones para esto primero; para una energía en boca de cañón igual dada, una bola más ligera, tendrá que moverse más rápido que la más pesada. Dado que la fuerza de resistencia, aumenta exponencialmente con respecto a la velocidad, una velocidad más alta proporcionará una fuerza de resistencia mucho mayor que una más ligera. Es decir, para energías cinéticas iguales, la fuerza de resistencia experimentada por un proyectil más ligero será mucho mayor que la de un proyectil más pesado. Además, la masa es un componente inverso para calcular la desaceleración debida a la resistencia. En otras palabras, a medida que aumenta la masa del proyectil, la desaceleración debida a la resistencia disminuye y se extiende el alcance. 

Para ilustrar esto, aquí hay gráficos que representan la desaceleración y la fuerza de resistencia experimentada por una bola de de 0.20g y una 0.25g disparadas a 0.75 julios (ó 285 y 255 fps respectivamente). En la Figura VIII-01, podemos ver que la resistencia experimentada por la bola de 0.20g es inicialmente mucho mayor, que la experimentada por la bola de de 0.25g. Aproximadamente a 53 pies, la fuerza de resistencia para ambas bolas es igual. Esto se debe simplemente a que la ecuación de la resistencia no tiene en cuenta la masa, sino que se rige principalmente por la velocidad. A una distancia de aproximadamente 53 pies, ambas bolas se mueven a aproximadamente 165 fps, por lo tanto, experimentan la misma fuerza de resistencia a esa distancia. 

La aceleración, sin embargo, depende de la masa. Hasta aproximadamente los 100 pies, la bola de 0.20g experimenta una mayor desaceleración que la de 0.25g, e inicialmente, la de 0.20g experimenta una desaceleración que es un 60% mayor que la experimentada por la de 0.25g. 

Todo esto puede parecer un poco confuso, porque estamos discutiendo tanto la fuerza como la aceleración. Para ponerlo en perspectiva numéricamente, aquí están los cálculos para la resistencia instantánea y la aceleración instantánea para tres bolas diferentes, proyectiles A, B, y C:

Los proyectiles A y B se disparan con energías iguales. Debido a que B tiene una masa mayor de 0.25 g, alcanza 0.75 julios a una velocidad más lenta en comparación con la masa de 0.20 g de A. Debido a que B se mueve más lentamente, experimenta menos fuerza de resistencia (lo que a su vez contribuye a una desaceleración menor). Sin embargo, tenga en cuenta que los proyectiles A y C se mueven a la misma velocidad (y debido a que C tiene más masa, tiene más energía). Las fuerzas de resistencia, que son independientes de la masa, son iguales para ambas bolas a la misma velocidad. La desaceleración de C, sin embargo, es menor porque la aceleración es una función de la masa. 

En la Figura VIII-03, podemos ver que para bolas sin efecto de hop-up, las bolas de 0.25 g eventualmente superan a sus contrapartes más ligeras. Sin embargo, lo más importante es observar que la diferencia es tan pequeña que sería casi imposible a simple vista de observar. 

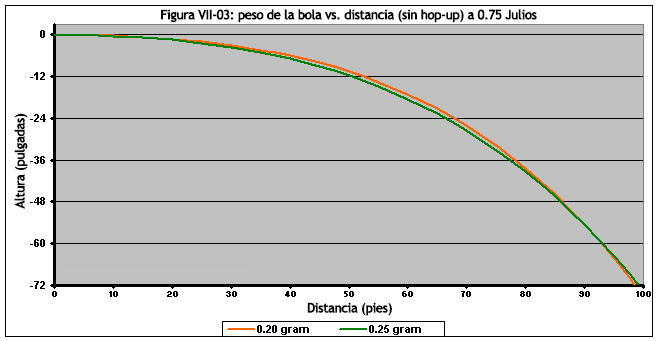
Cuando se aplica el hop-up, las bolas de menor peso pueden usar el contragiro para generar más elevación que las bolas más pesadas. Por supuesto, las bolas más ligeras también pierden este efecto de contragiro de manera más rápida que las bolas más pesados, lo que significa que los efectos del levantamiento disminuyen rápidamente. En definitiva, lo que sucede es que ambos tipos de bola experimentan trayectorias similares. 

En otras palabras, no hay una respuesta fácil a la pregunta de qué bola llega más lejos. Francamente, gran parte de la respuesta se reduce a la semántica, es decir, lo que describimos como "alcance efectivo". En la Figura VIII-04, vemos los efectos del hop-up en los mismas bolas de 0.20g y 0.25g que las anteriores. Si consideramos el "alcance efectivo", como la distancia a la que una bola experimenta la menor desviación del punto de su objetivo a 100 pies/30.4 metros, entonces ambas bolas funcionan de manera similar. Si un jugador está usando un rifle de francotirador y apunta a un objetivo que está a 140 pies/42.6 metros de distancia, y considera que este es el alcance efectivo para su rifle de francotirador usando el remanente, entonces la bola de 0.25g llegará más lejos. Una vez más, no hay una respuesta clara, sino que depende de lo que el jugador defina como "alcance efectivo". (Y... sería difícil ver la diferencia en la trayectoria entre las dos bolas ya que las trayectorias son muy similares). 

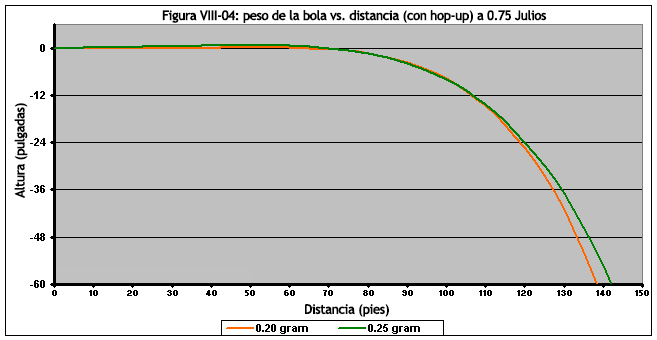
Lo más importante es que las bolas más pesadas no se traducen en una pérdida de alcance. En el peor de los casos, la trayectoria está a la par con sus contrapartes más ligeras, y la mayoría de las veces, las bolas más pesadas ​​superarán a las más ligeras. 

En la Figura VIII-05, vemos las trayectorias de bolas de 0.20g, 0.30g y 0.43g, disparadas a 2.32 julios. A una potencia tan alta, las bolas de 0.20g experimentan trayectorias salvajes. Si el jugador apunta por encima de su objetivo a más de 225 pies/68.5 metros, las bolas de 0.43g de hecho van más lejos, pero son las de 0.30g las que producen la trayectoria deseada. 

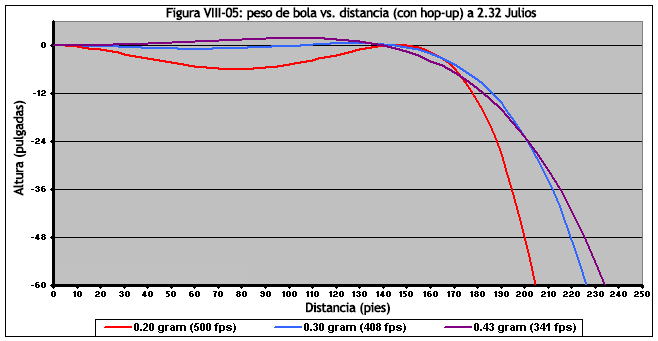
Un mejor ejemplo de la forma en que las bolas más pesados sobrepasan en distancia a las más ligeros, es mirar las trayectorias de varios pesos disparados en ángulo sobre el horizonte. Aunque no tiene importancia práctica, en la Figura VIII-06 podemos ver claramente que las bolas más pesadas ​​producen alcances mayores.   

En última instancia, las bolas más pesadas ​​superarán a sus homólogas más ligeras. Esto no significa que las municiones más pesadas sean siempre las bolas más útiles o necesarias. 

¿Qué peso de bolas llega al objetivo más rápido para una velocidad dada? 

En rangos de menos de 100 pies/30.4 metros, todos las bolas que pesan entre 0.20g y 0.43g alcanzan sus objetivos aproximadamente al mismo tiempo (suponiendo energías en boca de cañón iguales). En la Figura VIII-07, podemos ver los tiempos de vuelo de varias bolas disparadas a 0.75 julios. Todos alcanzan sus objetivos aproximadamente al mismo tiempo. Por ejemplo, una bola de 0.20g alcanza 70 pies/21.3 metros en aproximadamente 0.37 segundos, mientras que la de 0.25g alcanza la misma distancia en aproximadamente 0.38 segundos, la diferencia de tiempo apenas se nota. Alrededor de los 110 pies/33.5 metros, podemos ver que los proyectiles más pesados ​​están alcanzando sus objetivos un poco más rápido. A 140 pies/42.6 metros, una bola de 0.25g alcanzaría su objetivo aproximadamente 0.10 segundos más rápido que la de 0.20g. Como puede verse, la diferencia es insignificante. 

En rifles de alta potencia, la diferencia en el tiempo de vuelo apenas se nota en rangos de menos de 120 pies/36.5 metros. En la Figura VIII-08, podemos ver que la diferencia de tiempo solo se vuelve realmente notable a 155 pies/47.2 metros, donde una bola de 0.30g alcanzaría su objetivo aproximadamente 0.20 segundos más rápido que una de 0.20g. Nuevamente, esto se nota en la tabla, pero 0,20 segundos pasan bastante rápido cuando se dispara.

Así que si quieres una respuesta corta y fácil, sería esta:

A distancias inferiores a 125 pies/38.1 metros, todas los pesos de bola alcanzan su objetivo al mismo tiempo si se disparan con las mismas energías en boca de cañón. Más allá de 125 pies/38.1 metros, las bolas más pesadas, generalmente llegarán al objetivo más rápido que las más ligeras.

Determinar qué peso de bola alcanza su objetivo más rápido o qué peso de bola va más lejos, requiere cálculos y una respuesta complicada. Sin embargo, determinar si las bolas más pesadas ​​retienen su energía más tiempo, tiene una respuesta fácil y directa que siempre será cierta:

Suponiendo que una bola pesada y uno ligera están siendo disparados con las mismas energías en boca de cañón, la bola más ligera siempre, siempre, siempre experimentará una disipación de energía más rápida. 

Como se explicó con anterioridad, para una energía en boca de cañón dada, una bola más ligera, comenzará a viajar más rápido. Debido a esto, se desacelerará mucho más rápidamente en comparación con una bola más pesada. Podemos ver la disipación de energía en la Figura VIII-09. En este caso, estamos viendo varios pesos de munición disparadas desde un rifle Tokio Marui, con una energía de boca de 0,75 julios (con el disparo de 0.20g a 285 fps, el de 0.25g a 255 fps y el de 0.30g a 233 fps). Observa en la gráfica cómo la bola más pesada ​​retiene su energía mucho mejor. 

Esto es muy importante al determinar las distancias minimas de seguridad, y se explica con mayor detalle en la Sección VI: Distancias mínimas de seguridad.

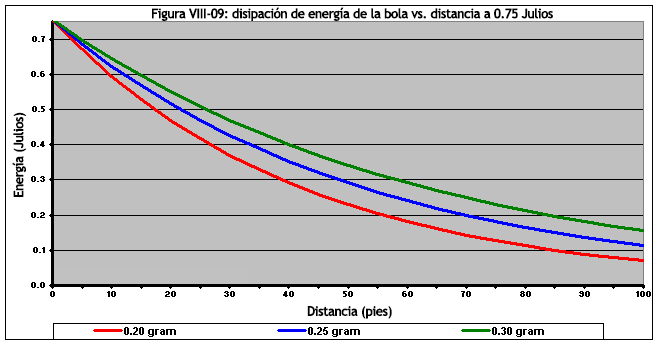
Ten en cuenta que esto solo es cierto cuando se comparan bolas de 6mm con otras de su mismo calibre. El área normal cambia, cuando se habla de bolas de 8 mm, sin embargo, una bola de 0.34g de 8 mm siempre perderá energía mucho más rápidamente en comparación que una bola de 0.45g de 8 mm.

¿Es necesario restringir un rifle con una velocidad de salida en boca de 600 fps a una distancia mínima de juego de 100 pies/30.4 metros?

Como se discutió anteriormente (y se discutió muy a fondo en la Sección VI-C: Distancias recomendadas universales), todo depende de la bola que esté usando el jugador. 

Tomemos el ejemplo de un rifle disparando a 3.35 julios, con disipación de energía representada en la Figura VIII-10. Si un campo de juego desea basar sus DMS (Distancia Mínima de Seguridad), utilizando una energía de impacto máxima de 1 julio, entonces un jugador que dispara una bola de 0.20g a 3.35 julios (ó 600 fps) necesitaría un DMS de sólo... 50 pies/15.2 metros. Sin embargo, si el mismo jugador disparara bolas de 0.43g a 3.35 Joules (o 409 fps con bolas de 0.43g), entonces la DMS necesitaría extenderse a ... 108 pies/32.9 metros, más del doble de la distancia necesaria para el disparo con bolas de 0.20g. 

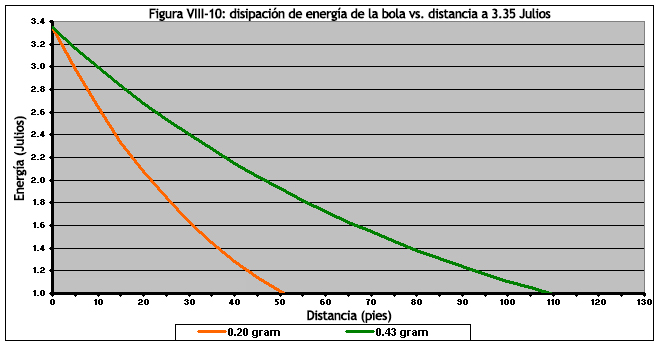
La razón principal por la que divido las DMS basadas ​​en el peso de la bola, es que el peso (o masa, técnicamente, pero ya sabes a lo que me refiero) hace una gran diferencia en la disipación de energía. Si un campo de juego desea imponer unas DMS para rifles, que se cronometran a 500 fps con bolas de 0.20g, entonces podrían restringir las DMS a 80 pies/24.3 metros para cualquier peso de bola, o usar unas DMS de 55 pies/16.7 metros y restringir el peso máximo de las bolas de a 0.30g (aunque habría que confiar en que todos los francotiradores estarían usando este peso de bolas, en términos de garantizar que no utilizan un peso de bola por encima de 0.30g). 

Para ver cómo los diferentes clases de peso de bola se traducen en diferentes DMS, use la calculadora provista en la Sección X-B: Calculadora de distancia mínima de seguridad/energía relativa. Incluso un rifle a 1.49 julios (400 fps con bolas de 0.20g), tiene diferentes DMS, ya sea que use bolas de 0.20g o 0.25g. 

Nuevamente, es una respuesta complicada, sin embargo, se responde en su totalidad en la Sección VI-C: Distancias recomendadas universales, completa con tablas imprimibles. Si tienes preguntas, o deseas asesoramiento o gráficas de cálculo personalizadaspara tu campo de airsoft, puedes contactarme por email.

¿Anulan mejor las bolas de 0.43g los efectos del viento mucho mejor que las bolas de 0.20 gramos?

Esta es otra fácil. Las bolas más pesadas ​​siempre mantienen su trayectoria mejor que las más ligeros, en el viento. Lo hacen por las razones discutidas anteriormente en donde aprendimos que la aceleración es inversamente proporcional a la masa. A medida que aumenta la masa del proyectil, la aceleración lateral disminuye, lo que significa que las bolas más pesadas ​​experimentarán menos deriva en comparación con las bolas más ligeras. Todo esto se explica con detalle en la Sección V-A-02: Componente viento cruzado y se muestra más abajo en la Figura VIII-11. 

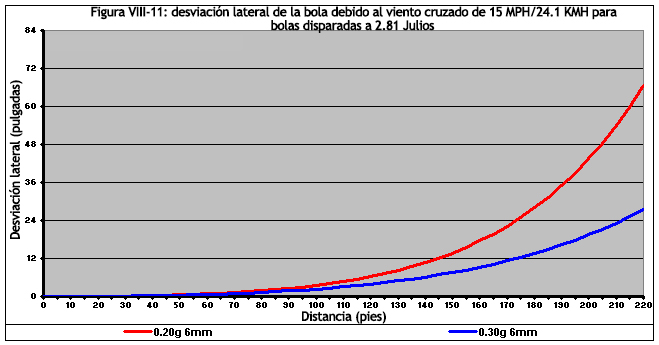
Aquí podemos ver los efectos de un viento cruzado de 15 millas por hora/24.1 kmh, en un rifle disparando a 2.81 Julios. En un rango de 220 pies/67 metros, una bola de 0.30g se habrá desplazado un poco más de 2 pies/60 cm lateralmente al objetivo, mientras que una de 0.20g se habrá desviado más de 5 pies/1.5 metros de manera lateral. El uso de bolas más pesadas de manera progresiva, ​​produciría una menor desviación lateral, sin embargo, observaría una ley de rendimientos decrecientes, como se muestra en la Sección V-A-02: Componente viento cruzado.

En resumen, definitivamente es posible acertar a un blanco a 300 pies/91.4 metros. 

Después de resolver el problema en términos de teoría y algunas pruebas con mi propio rifle, es muy posible el llegar a 300 pies/91.4 metros, y los francotiradores de airsoft están logrando eliminaciones a esas distancias y más allá. Dicho esto, sigo siendo pesimista porque dudo que un jugador pueda acertar rutinariamente un objetivo a esa distancia. El alcance más largo que he logrado, observado o verificado para golpear un objetivo de 18 pulgadas/45 cm de diámetro consistentemente, es de 235 pies/71.6 metros. Eso no quiere decir que haya distancias imposibles, sino que este es el rango efectivo más alto que he observado de primera mano. Tu experiencia puede ser diferente...

Si un tirador tiene un rifle altamente upgradeado, puede extender su alcance a 300 pies/91.4 metros, apuntando por encima del objetivo. Tomemos, por ejemplo, un tirador con un rifle a 3.35 Julios, disparando a un objetivo a 300 pies/91.4 metros de distancia. La Figura VIII-12 muestra la trayectoria de un disparo de 3.35 Julios, utilizando bolas de 0.36g. En este caso, el tirador necesitaría apuntar casi 7 pies/2.1 metros por encima de su objetivo. De nuevo, el rifle debería de ser muy consistente, y el tirador debería tener toda la suerte de su lado, pero es definitivamente posible (y... un disparo de 300 pies/91.4 metros, sería muy, muy poco probable con bolas de 0.20g o 0.25g.).

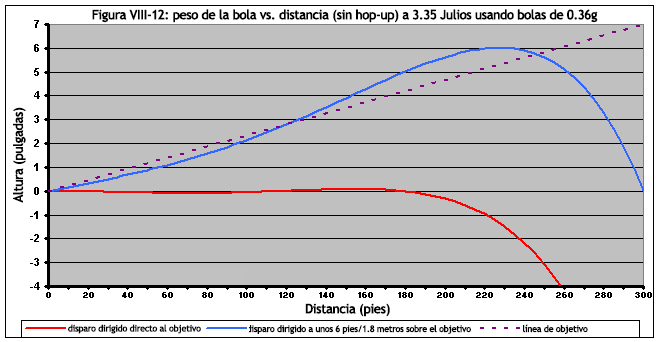
Otra cosa que el tirador debe darse cuenta, es que la energía de impacto a 300 pies/91.4 metros, se reducirá enormemente. En el caso del rifle 3.35 Julios disparando bolas de 0.36g, la energía de impacto de ese disparo en un rango de 300 pies/91.4 metros, sería de aproximadamente 0.06 Julios. En nuestras pruebas, descubrimos que las bolas alcanzan el objetivo a 0.06 julios, rebotando en una hoja de papel estándar (típicamente sin dejar siquiera una marca) y sería casi imposible de sentir este impacto. 

The short, simple answer is "nope." 

Sin embargo, como la mayoría de las cosas, este es un tema que requiere un poco de interpretación. El primero es una comparación de las bolas disparadas a 2,32 julios, o el equivalente a 500 fps con bolas de 0.20g. Para las bolas examinadas, esto sería equivalente a 408 fps con 0.30g y 6 mm, 384 fps con 0.34g y 8 mm, y finalmente 333 fps con 0.45g y 8 mm. La figura VIII-13 muestra las trayectorias:

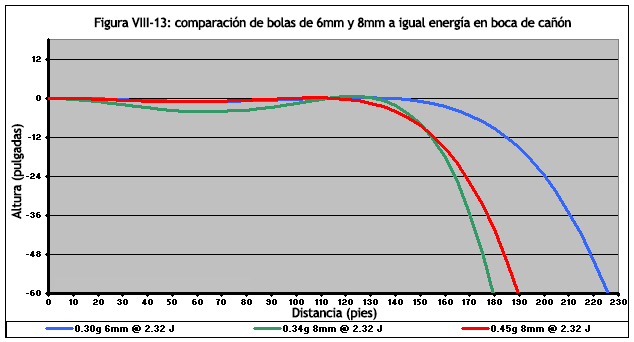
Es bastante obvio que, para energías en boca de cañón equivalentes, la bola de menor peso de 6 mm en realidad produce un mayor alcance. Más específicamente, la de de 6 mm va unos 25 pies/7.62 metros más que la bola de 0.45g y 8 mm, y unos 30 pies/9.1 metros más que la bola de 0.34g y 8 mm. 

Una cosa que debe considerarse aquí, es el hecho de que las bolas de 8 mm disipan la velocidad, y en consecuencia la energía, a una velocidad mucho más rápida que las de 6 mm. En otras palabras, las bolas de 6 mm, en el caso anterior, requieren mayores DMS. La bola de 0.30g y 6 mm, necesitaría un DMS de 53 pies/16.1 metros, mientras que la bola de de 0.45g y 8 mm necesitaría una DMS de 45 pies/13.7 metros, y en el caso de la de 0.34g y 8mm necesitaría una DMS de solo 38 pies/11.5 metros. 

Un problema que le veo a los campos que hay en USA, es que a las bolas de 8mm se les da un tratamiento equivalente, o en algunos casos, mayores DMS, cuando se las compara con las bolas de 6mm. Imagine un campo de juego que restringe las velocidades en boca a menos de 500 fps y le da una DMS para esos rifles de 55 pies/16.7 metros. Un jugador de airsoft aparece con un rifle de 8 mm que dispara bolas de 0.34g de 8 mm a 487 fps (la friolera de 3,75 julios). La mayoría de los campos de juego no permitirían este rifle en sus instalaciones. En realidad, si el campo de juego considera que un rifle de 500 fps está bien con una DMS de 55 pies/16.7 metros, entonces los 487 fps serán igual de seguros con la misma DMS: a 55 pies/16.7 metros, ambos tendrían una energía de impacto de 1 Julio (y la bola de 8 mm sería en última instancia aún más seguro porque la energía se dispersa en un área mayor).  (para aprender más sobre las DMS, y para ver las DMS recomendadas mínimas basadas en la energía en boca de cañón, pesos de bola y tamaños, consulta la Sección VI-C: Distancias recomendadas universales).

Todo eso quiere decir que la comparación de las bolas de 6 mm con las de 8 mm en función de las energías em boca de cañón, coloca a las de 8 mm en una desventaja injusta (y ten en cuenta que no soy usuario de 8 mm, y no hago estas declaraciones basadas en prejuicios, sino más bien en un esfuerzo por garantizar tanto la seguridad como la equidad en el airsoft). Una mejor comparación de bolas de 6mm con las de 8 mm sería una fuera de las DMS impuestas. 

Como se dijo con anterioridad, un rifle de 500 fps disparando bolas de 0.30g y 6 mm, tendría una DMS de 55 pies/16.7 metros. Para que una bola de 0.34 g de 8 mm tenga un DMS de 55 pies, se debe disparar a 487 fps (3,75 Julios), y una bola de 0.45g de 8 mm se debe disparar a 360 fps (2,71 Julios). La figura VIII-14 representa las trayectorias de las tres bolas.

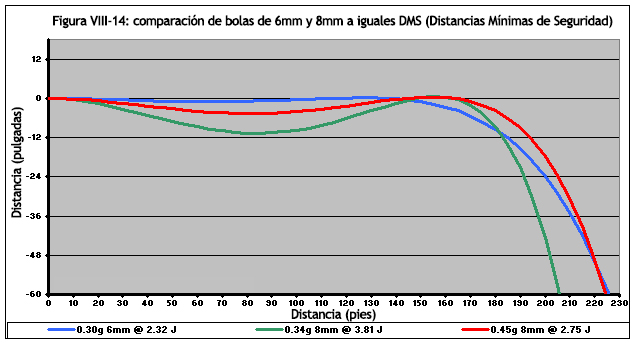
Incluso con DMS iguales, la bola de 6 mm todavía supera a la de 8 mm, sin embargo, ambos están mucho más cerca ahora. Debido a que las bolas de 8 mm son más consistentes y requieren un giro menor debido al hop-up para lograr la trayectoria deseada (y porque las bolas de 8 mm son menos propensos a volar errantes debido a imperfecciones de la superficie), las de 8 mm alcanzarían una mayor consistencia en la fase terminal de sus trayectorias. Aun así, dado el rango adicional (y el estándar de precisión de algunos bolas de 6 mm de alta calidad), considero que el alcance efectivo de la bola de 6 mm siempre es mayor que la de 8 mm.

Por la misma razón que las bolas de 8mm disipan la velocidad a una velocidad mucho mayor que las de 6mm, las de 8mm también experimentan una mayor desviación lateral debido a un viento cruzado. Una cosa a tener en cuenta es que las bolas de 8mm son menos densas en comparación con las de 6mm (para detalles, pásate por la Sección I-A-02: Densidad/Volumen). Además, la mayor superficie de las bolas de 8mm, significa que la resistencia lateral debido al viento será mayor que las bolas de 6mm. 

La Figura VIII-15 muestra la desviación lateral de varias bolas de 6mm y 8mm, disparados a 2.81 Julios, en un viento cruzado de 15 millas por hora/24.1 kmh. 

En una distancia de 200 pies/60.9 metros, las bolas de 6 mm solo se han desviado entre 1 y 2 pies/30-60 cm desde el punto de objetivo. La bola de 0.45g y 8mm, en comparación, se ha desviado casi 4 pies/1.2 metros, y la bola de 0.34g y 8mm BB se ha desviado casi 7 pies/2.1 metros. Incluso si compararas la bola de 0.45g y 8 mm con la de 0.20g y 6 mm, la de 0.20g y 6mm, todavía mantiene su trayectoria mejor en términos de desviación lateral (la deflexión de la bola de 0.20g y 6mm está por encima).

En resumen, las bolas de 6mm resisten los efectos del viento cruzado MUCHO mejor que las de 8mm. 

Las bolas a alta velocidad NO resisten el viento mejor que las que van a baja velocidad. Por el contrario, las bolas a alta velocidad, alcanzan su objetivo más rápido que las que van a baja velocidad, lo que significa que hay menos tiempo para que el viento desvíe una bola a alta velocidad. 

Para explicarlo mejor, aquí hay un gráfico con texto tomado directamente de la Sección V-A-02: Componente viento cruzado:

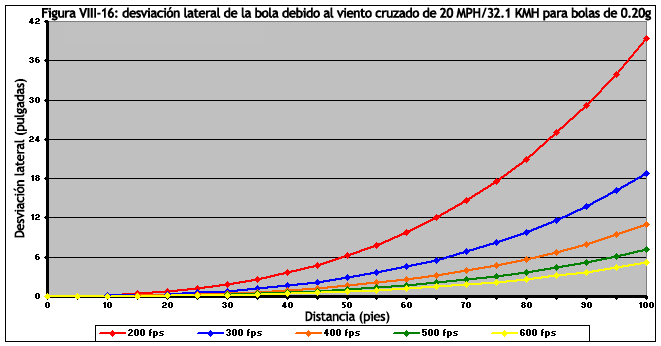
La Figura VIII-16 muestra cómo la relación entre la velocidad en boca de cañón y el viento cruzado. Podemos ver que para pesos de bola iguales, un disparo de alta potencia alcanzará su objetivo al experimentar menos desviación. Por ejemplo, si disparas a un objetivo a 100 pies/30.4 metros de distancia con un viento cruzado de 20 mph/32.1 kmh, una bola de 0.20g disparada a 400 fps, solo se habrá desviado 11 pulgadas/27.9 cm, mientras que un disparo de 300 fps se habría desviado alrededor de 19 pulgadas/48.2 cm. 

Tenga en cuenta que durante un período de tiempo igual, la bola se mueve lateralmente la misma distancia para cada disparo. Los disparos de alta potencia no resisten el viento cruzado mejor que los disparos de baja potencia; más bien, los disparos de alta potencia llegan más lejos en menos tiempo. Para explicarlo mejor, un disparo de 600 fps alcanza los 100 pies/30.4 metros después de 0,32 segundos, después de lo cual se ha desviado aproximadamente 5 pulgadas/12.7 cm. Después de 0,32 segundos, el disparo de 500 fps solo ha recorrido 90 pies/27.4 metros, donde tiene una desviación igual de 5 pulgadas/12.7 cm. Por el contrario, el disparo de 200 fps solo alcanza unos 47 pies/14.3 metros en el transcurso de esos 0,32 segundos.